This tutorial walks through how you can deploy WordPress on a CS Department Server.
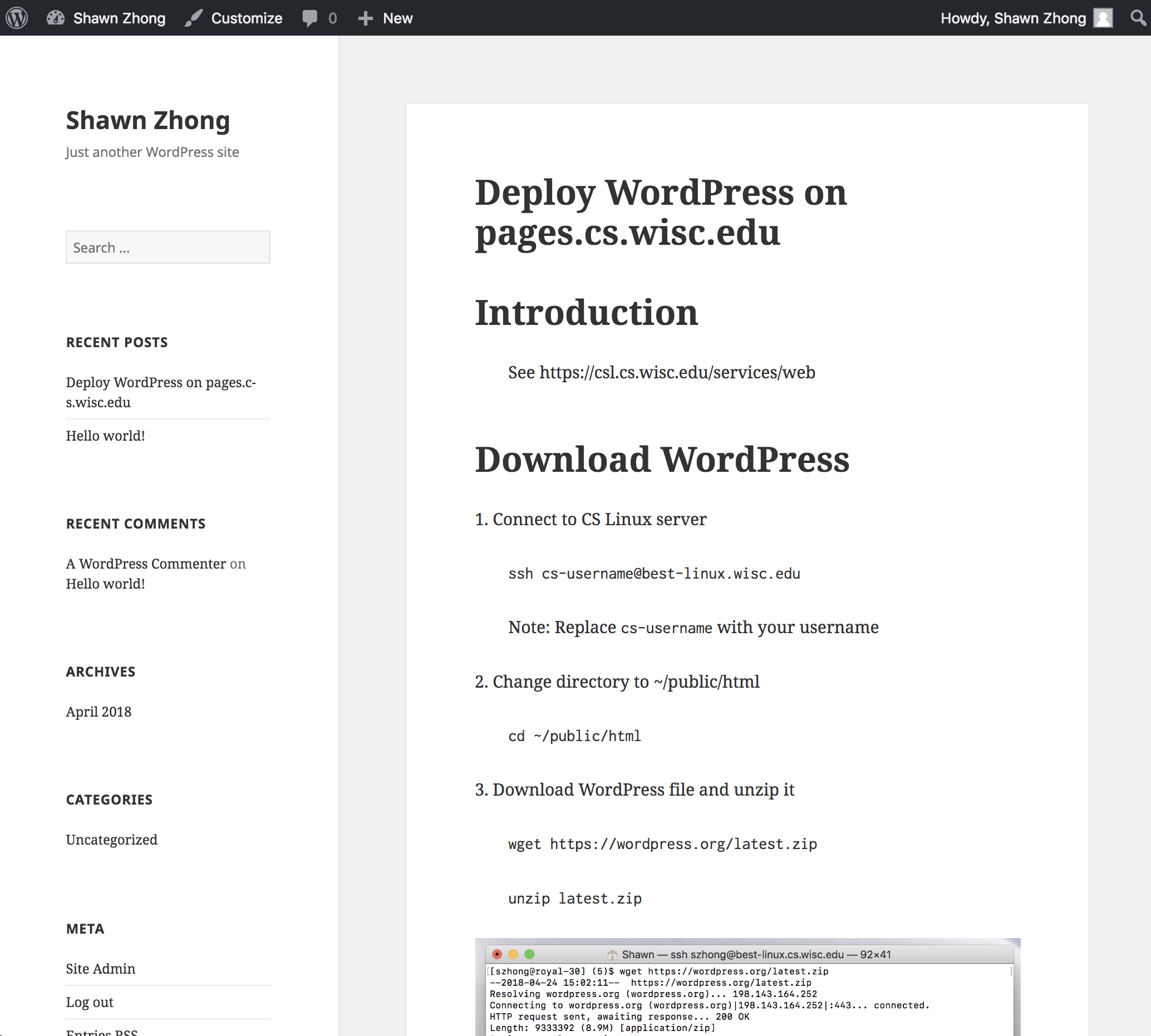 (more…)
(more…)
 (more…)
(more…)